power of research is accept null hypothesis when it's true
- related: Biostats
- tags: #literature #boards
Hypothesis testing is important when performing empirical research and evidence-based medicine. There are two types of statistical hypotheses: the null and the alternative hypotheses. The null hypothesis is denoted by H0 and it is usually the hypothesis that sample observations result purely from chance. The alternative hypothesis, denoted by H1 or Ha, is the hypothesis that sample observations are influenced by some nonrandom causes. In any hypothesis testing, there are four possible outcomes (Figure 1). The power of the test is the probability that the test will reject the null hypothesis when, in fact, it is false (choice A is correct). Having a high value for 1 − β (near 1.0) means it is a good test, and having a low value (near 0.0) means it is a poor test. Conventionally, a test with a power of 0.8 is considered acceptable. In addition, when a test accepts the null hypothesis when it happens to be true, it is called confidence level denoted by (1 − α) (choice B is incorrect). A Type I error (also called the significance level and is usually denoted by α) occurs when the researcher rejects a null hypothesis when it is true (choice C is incorrect). A Type II error (also called β) occurs when the researcher accepts the null hypothesis that is false (choice D is incorrect).
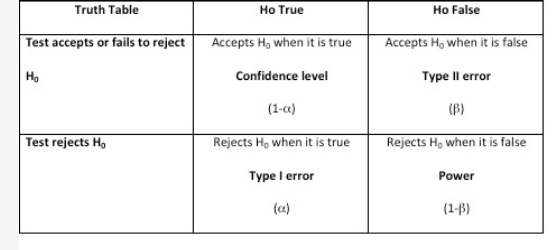Hypothesis Testing
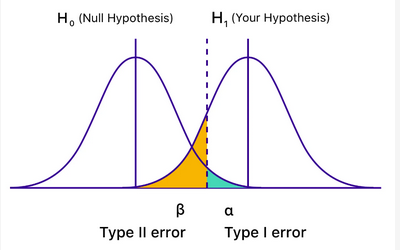
Type II error. Figure courtesy of the Mayo Foundation for Medical Education and Research.
Statistical analysis of various studies hinges on significance testing. Two types of sampling errors exist, known as type I and type II, and also termed α and β errors. A type I error is a false-positive conclusion, resulting from rejecting a null hypothesis that is correct. A type II error is a false-negative conclusion, meaning a failure to reject a null hypothesis that is false.
Type I errors are typically emphasized as the most important to avoid in statistical analyses, but the type I error (a false-positive conclusion) is actually only possible if the null hypothesis is true. If the null hypothesis is false, a type I error is impossible, but a type II error, the false-negative conclusion, can occur. One way to reduce type II statistical error is to increase the sample sizes of the cohorts studied (choice D is correct).
Alpha (α) represents the probability of type I error, meaning concluding there is a difference in the study subjects receiving each of the drugs you are studying, when in fact no difference actually exists. Beta (β) is the probability of type II error—that is, concluding there is no difference in study groups, when in fact there truly is a difference. The greater the statistical power of your study, the less the probability there is of making a type II error (Figure 1) (choice A is incorrect). Larger sample sizes in the studies after yours reduced sampling error and increased, not decreased, statistical power (choice B is incorrect). The data you reviewed in your clinical trial in this case led you to conclude that the null hypothesis of no difference between the two groups was valid when, in fact, you should have rejected the null hypothesis—in other words, you had a false-negative result. This represents type II, not type I, statistical error (choice C is incorrect).1
| A. | If your study had greater statistical power, there was greater probability of making a type II error. | 6.41% |
| B. | Larger sample sizes of more recent studies reduced sampling error but decreased statistical power. | 4.23% |
| C. | Your clinical trial was plagued by type I statistical error. | 14.87% |
| D. | One way to reduce type II statistical error in your study would have been to double the number of total subjects enrolled. |