calculating survival probability
- related: Biostats and Study Design
- tags: #literature #pulmonology
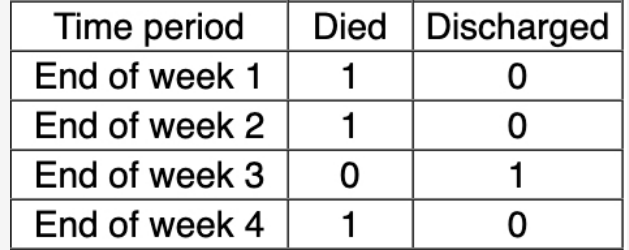
Survival probability is the number of patients surviving at a given time point divided by the number at risk. At the first time point, this is a simple probability. At each of the subsequent time points, the survival probability is the probability of surviving up to that time period and the probability of surviving to the end of that time period and therefore is a compound conditional probability. To estimate survival probability at the end of week 4, we must determine the compound conditional probability of surviving up to week 4. This means that we need to know how many patients survived at each time point and how many were at risk. Patients who are lost to follow-up or, in this instance, discharged from the ICU, are considered to have survived until the end of the time period at which they are discharged but then are “lost” and no longer considered “at risk” for the subsequent time period. A commonly used example of this methodology is Kaplan-Meier survival curves.

The number surviving, the number at risk, and the compound conditional probability of survival at each time period are shown in Figure 2.
The survival probability for patients with COVID-19 in this ICU is 60%. The total proportion of patients who survived to the end of week 4 is 5/8 or 62.5%. However, this is a proportion and not a probability. In corollary, the proportion of patients who died by the end of week 4 is 3/8 or 37.5%. Although the survival probability is 60%, the probability of death is 40% (1 − survival probability).1