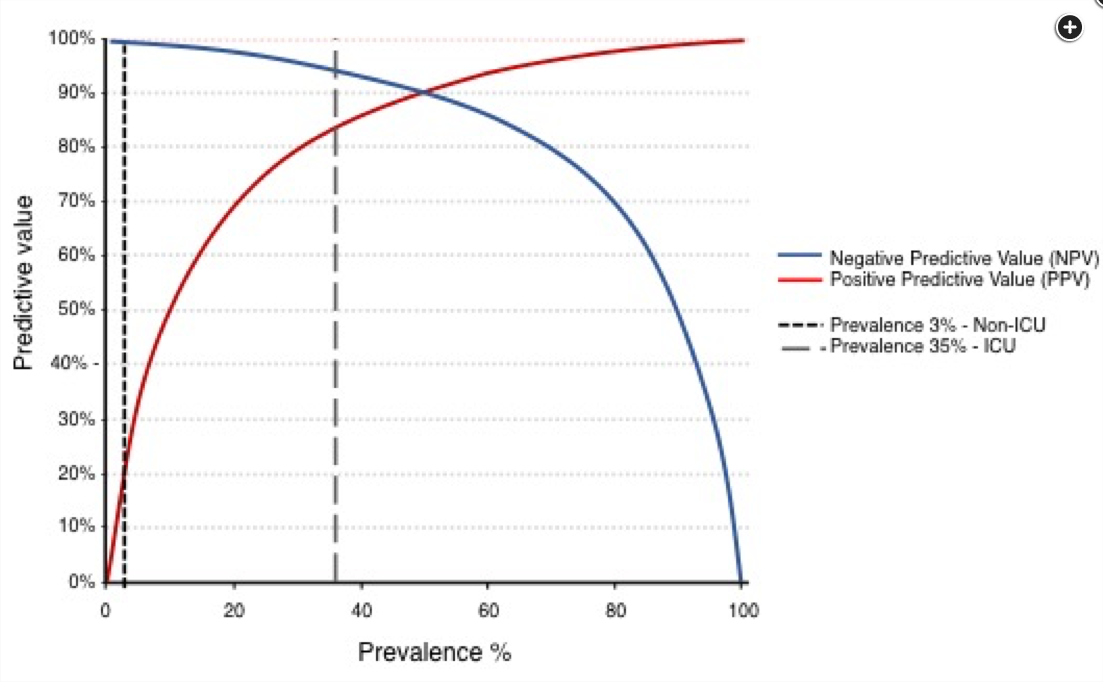
PPV has positive relationship with prevalence
- related: Biostats and Study Design
- tags: #literature #pulmonology
Applying test performance characteristics to a population where the disease prevalence is lower is likely to make the PPV lower and negative predictive value higher.
This example of lower prevalence (3%) of arterial or venous thrombotic complications in noncritically ill hospitalized patients increases the negative predictive value (NPV) of this novel test (choice A is correct; choices B, C, and D are incorrect). The general Bayes’ theorem states:
This applied to the NPVs results in:
As it can be derived by the previous formula, the lower the disease prevalence is, the higher the NPV is, and, consequently, the lower the positive predictive value (PPV) is:
A feature of PPV and NPV is their dependence on the prior probability of the disease (which is equal to the prevalence of disease in the population to be tested) (Figure 1). If the disease prevalence increases (as it occurs [35%] in the critically ill patients), a positive result will have a higher PPV. This is due to a relative decrease in the number of patients with false-positive results to the number of true-positive results (Figure 1). As a consequence, the proportion of true-positive results among the total number of those with a positive test result will rise, resulting in a higher PPV. The opposite will occur for NPV, in which high disease prevalence will result in a low NPV.